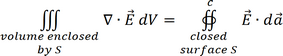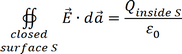In order to analyze the behavior of electrostatic transducers we will now refresh our memory on electromagnetic field theory and calculate the electric field and the energy stored in a parallel plate capacitor.
Figure 2.2.1 shows a schematic drawing of a parallel plate capacitor with a surface charge density +σ and –σ (in [C/m2]) on the inner surface of the conducting plates. As long as the distance d between the plates is much smaller that the plate dimensions we can treat the structure as if the plates were infinitely large. In that case, the electric field E will be directed perpendicularly from one plate to the other as indicated in the figure. We can easily calculate the field starting from the Maxwell equations for electrostatics, i.e. neglecting all time dependent terms:
|
(2.1) |
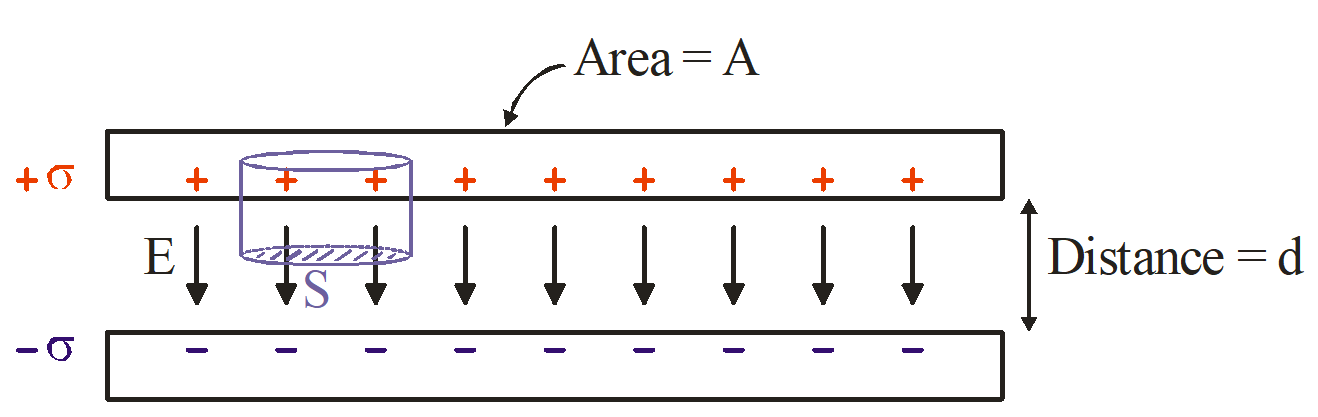
Figure 2.2.1: Schematic drawing of a parallel plate capacitor.
Applying Gauss’ theorem:
|
(2.2) |
We can write the first equation in its integral form:
|
(2.3) |
That is, the flux of E out of any closed surface S will be proportional to the total charge inside the volume enclosed by S. The field E can now be calculated by considering a suitable closed surface S. For example, one can consider the cylindrical surface indicated in Figure 2.2.1, with one end inside a conductor (where the electric field has to be zero) and the other end in the region between the plates. The flux of E through the surface is now defined completely by the bottom surface of the cylinder (the shaded part in Figure 2.2.1). The total charge inside the cylinder is equal to σ times a surface with exactly the same size. It now immediately follows that:
|
(2.4) |
Once we know the electric field, we can also calculate the potential difference u between the two plates, which is simply the path integral over the field from one plate to the other:
|
(2.5) |
Furthermore, the capacitance is defined as the ratio between the charge on the capacitor and the voltage between the plates, so:
|
(2.6) |
We can also calculate the amount of energy stored in the capacitor, since the energy stored in the electric field is given by:
|
(2.7) |
Integrating the electric field over the volume between the plates we find:
|
(2.8) |
From (2.8) we can conclude that we can change the energy stored in the capacitor in two ways: electrically, by changing the amount of charge on the capacitor plates, or mechanically, by changing the capacitance value. The latter can be done in several ways:
•By changing the distance d between the plates.
•By changing the (overlap) area A of the plates.
•By changing the medium between the plates (i.e. changing ε), e.g. by allowing a dielectric to move between the plates.