<< Click to Display Table of Contents >> Navigation:  Part 2: Electrostatic Transducers I > 2.3 Force and voltage

From electromagnetic field theory we know that the force on a charge q in an electric field E is given by:

And, therefore, the work we need to do to move a charge from a point (a) to a point (b) in the field is given by:

where u is the potential difference between the two points. The minus sign is because the force we need to apply is in the opposite direction of the force acting on the charge due to the electric field.

From (2.10) we see that the work needed to move a small amount of charge dq from one capacitor plate to the other is given by:

This work dW of course has to be equal to the increase in energy dU stored in the capacitor. So, integrating (2.11) we get the same result as in (2.8):

If we now also allow the capacitance to change we have to include the work needed for this in our analysis. For the sake of simplicity, let us assume that only the distance between the plates can change. In that case, we can write the capacitance as:

where we now use the symbol x for the distance between the plates.

The work needed to move the capacitor plate over a small distance dx is given by:

where Fext is the force that we need to apply (hence the subscript ext for ‘external’), which is opposite to the internal force that the system exerts on the plate.

To calculate the total energy stored in, what is now a transducer with one port to the electrical domain (dW=udq) and one port in the mechanical domain (dW=Fext dx), we have to consider the work done at both ports. The increase in the energy stored in the transducer is the sum of the work done at the ports:

Again, we can find the total energy stored in the transducer by integrating (2.15), however the integral is now a little more complicated than (2.12), because U is now a function of two variables: q and x. The latter means that we have to do a path integral from the point where both x=0 and q=0 up to the point (x, q) where we want to know the energy. For example, we could first integrate over x while keeping q equal to zero, and then integrate over q while keeping x constant. Mathematically we can write this as follows:

where the voltage u and the force Fext are also functions of both x and q. Figure 2.3.1 shows a graphical illustration of this path integral. In fact, we should also add an integration constant UA representing the energy already present in the transducer when x=0 and q=0, however, as we will see later, since we are only interested in derivatives of the energy function this does not make any difference and we may assume UA to be zero.

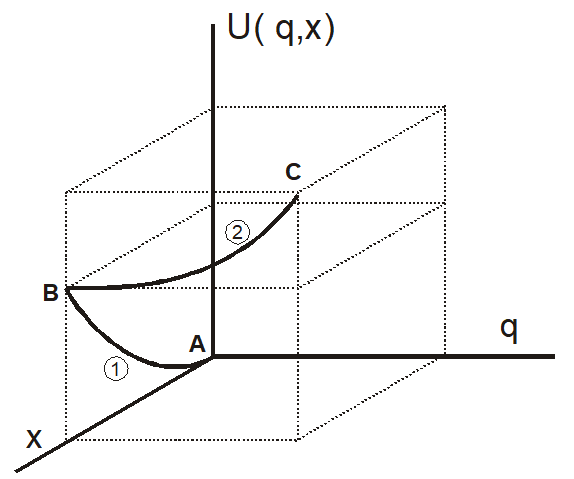
Figure 2.3.1: Graphical representation of the path integral (2.16). To find the energy stored in the transducer as a function of x and q we can integrate first over x (path 1), while keeping q equal to zero, and next over q (path 2) while keeping x constant. In fact we should also add an integration constant to represent the energy UA (in point A) already present in the transducer at x=0 and q=0. However, since UA is not dependent on x and q we are not really interested in it and usually omit it.

 

Doing the integration of equation (2.16) we find that, if there is nothing else than the two capacitor plates, the integral over x becomes zero because when q=0 there is no force needed to separate the plates. Therefore, we get exactly the same result as we got before:

In a more realistic situation where one of the capacitor plates is fixed and the other suspended by a spring the result will be different: even if q=0 we will still have the force due to the spring so that Fext is no longer equal to zero. We will treat this situation in the next section, but first we will show how (2.17) can be used to find the voltage u and the force Fext when x and q are known.

Like any function of two variables we can write the total differential of the energy function U(q, x) as follows:

Where is the partial derivative of U to x with constant q and is the partial derivative of U to q with constant x.

Comparing (2.15) and (2.18) it follows that

The external force is equal to the work, which is needed to separate the plates more from each other per unit length, keeping the charge constant. The voltage is the work needed to add charge on the plates per unit charge, keeping the distance constant.

Note that the subscripts q and x outside the brackets are very important. One can only calculate the derivatives if the dependency of U on q and x is explicitly given in the formula. It is quite easy to make mistakes. For example, one might use the relation between u and q, q=uC=u εA/x, to express the energy as a function of the voltage:

There is nothing wrong with doing this; however one should not take the derivative of (2.21) to find Fext. The result will have the wrong sign!

The problem is that u is a function of both q and x. The derivative of (2.21) is the derivative at constant voltage u and not at constant charge q. In section 2.5 we will see how we can do this correctly.