Figure 2.9.1 summarizes our approach so far: we start by calculating the energy function in terms of the extensive variables. Next, we find the intensive variables by partial differentiation. If the transducer is controlled by one (or both) of the intensive variables we then need to rewrite the result to have the extensive variables as the dependent variables.

Figure 2.9.1: Summary of the approach we have taken so far.
We will now discuss another approach in which it is possible to calculate the dependent variables directly by differentiation. For that, we have to construct a function from the energy function U(x, q), which is not a function of x and q, but of the two controlling variables. This function is called the Legendre transformation (Adrien Marie Legendre, French mathematician, 1752-1833). The basic idea of the Legendre transformation is to subtract the product of the intensive and the extensive variable from the energy function and rewrite the resulting expression in terms of the controlling variables. Thus, in the situation that a voltage is applied between the capacitor plates we subtract the product uq from the energy function and write the result in terms of u and x. We will call this new function U':
|
(2.40) |
The negative of this function, -U', is also known as co-energy. From the Legendre transform U' we can now calculate the charge q and force Fext by partial differentiation at constant voltage u and position x. The easiest way to show this is by looking at the total differential of :
|
(2.41) |
Inserting (2.15) for dU, the terms udq cancel out and we get:
|
(2.42) |
from which we immediately see that:
|
(2.43) |
|
(2.44) |
For an electrostatic transducer the Legendre transform U' is easily calculated by using q=Cu=uεA/x. We then have U=q2x/2εA=q2/2C=u2C/2, and uq=u2C, so
|
(2.45) |
Taking the derivative to x at constant u will give the external force
|
(2.46) |
WIth voltage control the force depends on the distance: it decreases inversely proportional to the square of x. The reason is that the amount of charge on the plates changes when changing the distance between the plates while keeping the voltage constant. A larger plate distance gives a smaller capacitance and at the same voltage there will be less charge on the capacitor.
The Legendre transform is generally valid. Always when you are dealing with functions with more than one variable it is indispensable. All transducers which transfer energy from one domain to another have to be described by functions with more than one variable, because the energy depends on variables in several physical domains. Note that in the case of a function of two variables, there are three different Legendre transformations. For electrostatic transducers these are:
|
(2.47) |
|
(2.48) |
|
(2.49) |
Summarizing, we can say that if a transducer is controlled by one of the intensive variables (in the case of an electrostatic transducer: the voltage u or force Fext) it may be useful to work with a Legendre transform of the energy function. The Legendre transform allows you to calculate the other two variables and the characteristic equations by taking simple partial derivatives. However, it must be noted that we can obtain the same results without using Legendre transformations: it is perfectly ok to start with the energy function U(x, q), calculate the voltage and force using the partial derivatives to x and q, and then rewriting the result to find the force as a function of x and u. We can choose either way, as illustrated in Figure 2.9.2.
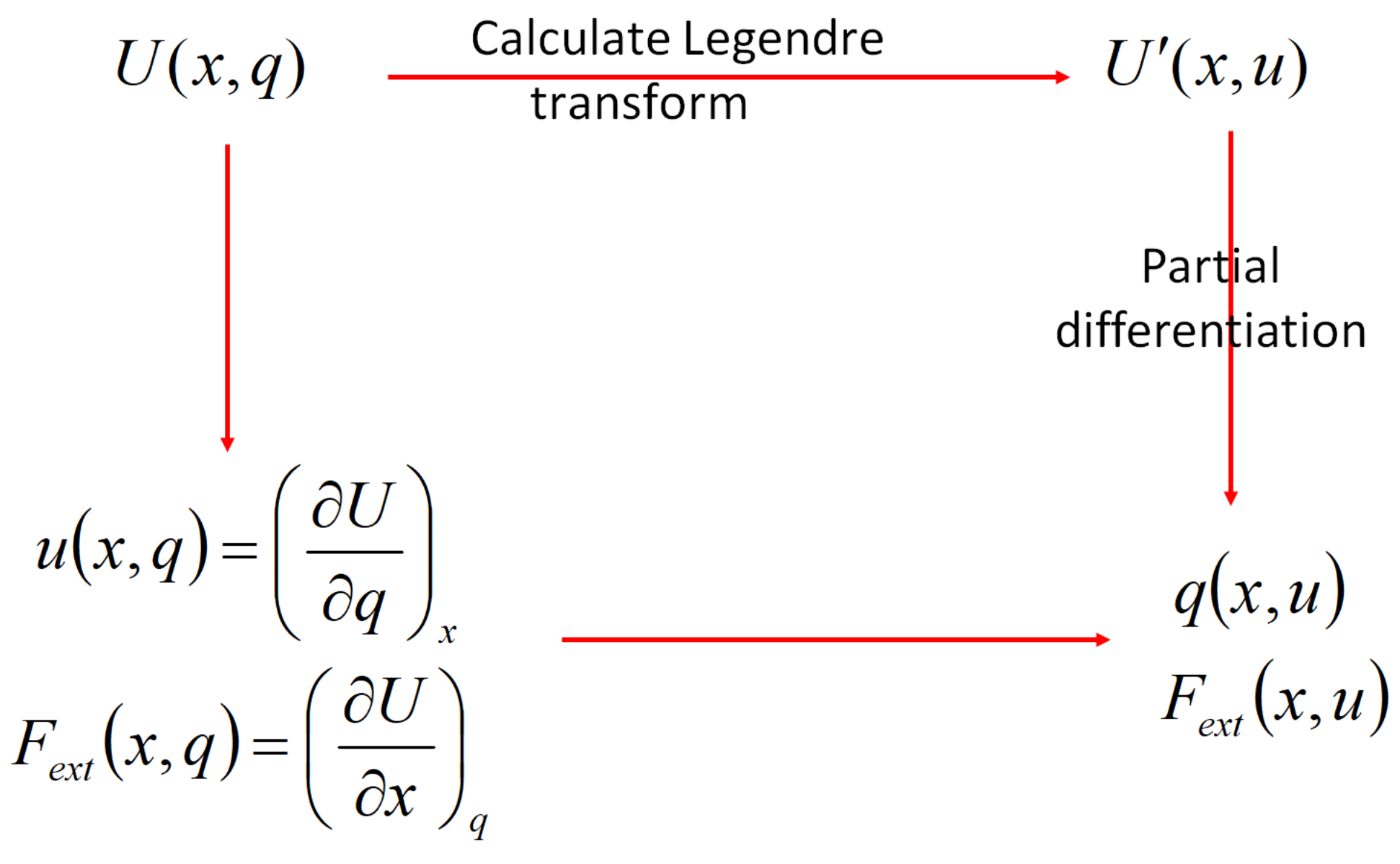
Figure 2.9.2: Alternate route by using the Legendre transform.