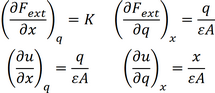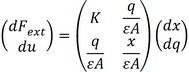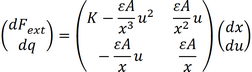Taking a closer look at the equations (2.26) and (2.27) in section 2.5 you see that both the force and the voltage are a function of x and q:
|
|
We can write the total differentials as follows:
|
(2.50) |
|
(2.51) |
These equations are called characteristic equations and are used to describe the small signal behaviour of the system, i.e. we can use them to relate small changes dx and dq around an equilibrium situation (x, q) to corresponding changes dFext and du.
In the case of the parallel plate capacitor with spring, Fext and u are given by (2.26) and (2.27), and we can easily calculate the partial derivatives in (2.50) and (2.51):
|
(2.52) |
It makes sense to reflect. The first derivative gives the effective spring constant. This is because the force between the plates (with a constant charge!) only depends on the position due to the presence of the spring. To move the plate one only has to oppose the spring force plus a constant electrostatic force. This is comparable with the situation of a mass on a spring hanging in the gravitational field of the earth, where you have a constant (position independent) gravitational force plus the spring force. In that case the derivative of the force with respect to position is also just the spring constant.
The last term in (2.52) is just the reciprocal capacitance. It relates small changes in q to small changes in u without changing the geometry (x is constant). So, with q=Cu this has to result in the reciprocal capacitance (1/C).
The other two terms can be read as follows. We are talking about how the force changes as a function of the charge leaving x constant and we are talking about how the voltage changes as a function of x, leaving the charge constant. Here we are dealing with two domains at the same time: these expressions say something about the transduction from one domain to the other. Note that the two expressions are equal to each other: this is no coincidence! When starting from the energy function U(x,q) these terms are obtained by taking the partial derivative to x and to q. It does not make any difference in which order the derivatives are taken.
It is often useful and providing insight to write the characteristic equations (2.50) and (2.51) in a matrix form. For the capacitor with spring this gives:
|
(2.53) |
In case of voltage control we can derive the characteristic equations starting from (2.30) and (2.31). In that case we find:
|
(2.54) |
We now recognize the effective spring constant at the top left and the capacitance in the lower right. These relate the variables within each domain to each other. Again the other two terms describe the transduction. Note that these terms are no longer equal to each other: one of them now has a minus sign!